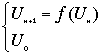La réintroduction du Vautour Fauve
Modèle mathématique utilisant les suites numériques

Introduction
Ce TD s'adresse aux élèves de première ou de terminale scientifique. Il s'agit d'une application des
suites récurrentes à la modélisation de l'évolution d'une population animale. L'utilisation de
la calculatrice pour représenter graphiquement les premiers termes d'une suite récurrente est conseillée.
Il se décompose en 2 parties :
Partie I : Construction d'un modèle représentant l'évolution de la population
Partie II : Exploitation de ce modèle afin de prévoir les conditions d'une réintroduction réussie
Partie I : Construction d'un modèle mathématique
Dans le Vercors, un projet de réintroduction du vautour fauve a été voté par les communes.
Une équipe scientifique a été chargée de mener une étude. Ce travail doit permettre de
déterminer le nombre de vautours à lâcher pour qu'une population stable s'établisse dans le Vercors.
Et si les scientifiques, c'étaient vous ? ! ! .....
Mise en place du problème
Introduisons des notations !
Appelons "l'année 0" le moment où l'on effectue cette réintroduction. On lâche alors
un nombre "U0" de vautours !
On appellera "U1" le nombre de vautours l'année suivante et de façon général, "Un"
le nombre de vautours au bout de n années.
Question :
Pour que la réintroduction réussisse, comment souhaite-t-on que se comporte la suite (Un) ?
Le problème, c'est que l'on ne connait pas cette suite (Un) ! ! ...
Mais peut-être pouvons-nous essayer de la déterminer ? ....
Pour rechercher la suite (Un), il faut traduire mathématiquement ce qui se produit dans la nature.
Premier modèle
On peut dans un premier temps, supposer que la population de vautours évolue géométriquement.
C'est à dire que la suite (Un) suit une relation de la forme :
r étant ce que l'on peut appeler le taux de renouvellement de la population
Question :
Seulement, nous ne connaissons pas la valeur de r.
Comment faire pour donner à r une valeur biologiquement réaliste ?
Question :
Que se passe-t-il si 0 < r < 1 ?
Que se passe-t-il si r > 1 ?
Que se passe-t-il si r = 1 ?
Question :
Ce modèle vous semble-t-il compatible avec ce qui peut réellement se passer dans la réalité ?
Deuxième modèle
On sent bien que dans la réalité, le taux de renouvellement d'une population varie d'une année à
l'autre.
Ce taux dépend en effet de la mortalité et de la natalité qui eux dépendent des conditions dans
lesquelles vit la population.
Question :
Supposons que la quantité de nourriture dont disposent les vautours soit limitée.
D'après vous, que va-t-il se passer si l'effectif de la population augmente ?
Comment va évoluer le taux de renouvellement ?
Pour représenter la réalité des choses, ll faut donc faire en sorte que r, le taux de renouvellement de la population, diminue si la population augmente. Et si nous exprimions r de la façon suivante :
a étant un réel représentant le taux de renouvellement maximum de la population. Dans les populations naturelles, on constate que ce taux est généralement compris entre 0 et 0,04
Question :
Comment évolue r si Un varie de 0 à 100 ?
Question :
Cette expression de r vous paraît-elle réaliste ?
Remarque :
Dans toute la suite, nous supposerons que l'effectif de la population ne peut dépasser 100 individus.
Nous avons donc obtenu un deuxième modèle pour décrire l'évolution de l'effectif de notre population.
Partie II : Exploitation du modèle
Nous venons de construire une suite qui doit nous permettre de prévoir l'évolution de notre population de
vautours. Je vous propose maintenant d'étudier son comportement. Nous verrons que selon la valeur choisie pour U0 ce
comportement peut être convergent, divergent ou même chaotique. Afin de réussir la réintroduction,
nous choisirons une valeur de U0 de telle façon que la suite (Un) converge vers une valeur non nulle.
L'étude analytique de (Un) est très difficile. Nous allons donc procéder graphiquement.
Appelons f la fonction : f(x) = a.(100 - x).x
Nous avons ainsi :
Etude graphique du comportement de (Un)
Traçons la courbe représentative de la fonction f et la droite y = x.
On prendra par exemple a = 0,016. D'où f(x) = 0,016.x(100-x)

Question :
Prenez par exemple : U0 = 80
En utilisant les 2 courbes précédentes, déterminez graphiquement les premiers termes de la suite (Un).
Question :
Que pensez-vous du comportement de la suite ?
Refaites le raisonnement précédent en considérant d'autres valeurs de U0.
Expérimentation
Ne connaissant pas à priori la valeur de a pour les vautours, nous allons étudier l'évolution
de la population en considérant plusieurs valeurs possibles de a.
Vous prendrez par exemple :
a = 0,008
a = 0,016
a = 0,02
a = 0,04
Question :
Pour chacune de ces valeurs, vous étudierez l'évolution de la population en utilisant la méthode vue précédemment. Vous pouvez utiliser votre calculatrice pour représenter graphiquement la suite correspondante (TI 82 au moins). Dans chaque cas, vous déterminerez ainsi, le nombre de vautours à lâcher pour que la population se stabilise (si c'est possible). C'est à dire, la valeur à donner à U0 .....
Question :
Discuter des chances de réussite de cette réintroduction.